2025年のAI業界は、まさにDeepSeekの年であったと言っても過言ではない。そして、その激動の年の暮れに、彼らは最後に大きなサプライズを用意していた。それが、新しいアーキテクチャ概念 「mHC (Manifold-Constrained Hyper-Connections)」 である。
これまでのTransformerの改良は、主にAttentionメカニズムの効率化(Linear AttentionやMLA: Multi-Head Latent Attentionなど)や、MoE(Mixture of Experts)のルーティング最適化に焦点が当てられてきた。しかし、今回の提案はより根源的な、ネットワーク内の「接続(Connection)」と「信号伝播の幾何学(Geometry)」にメスを入れるものである。
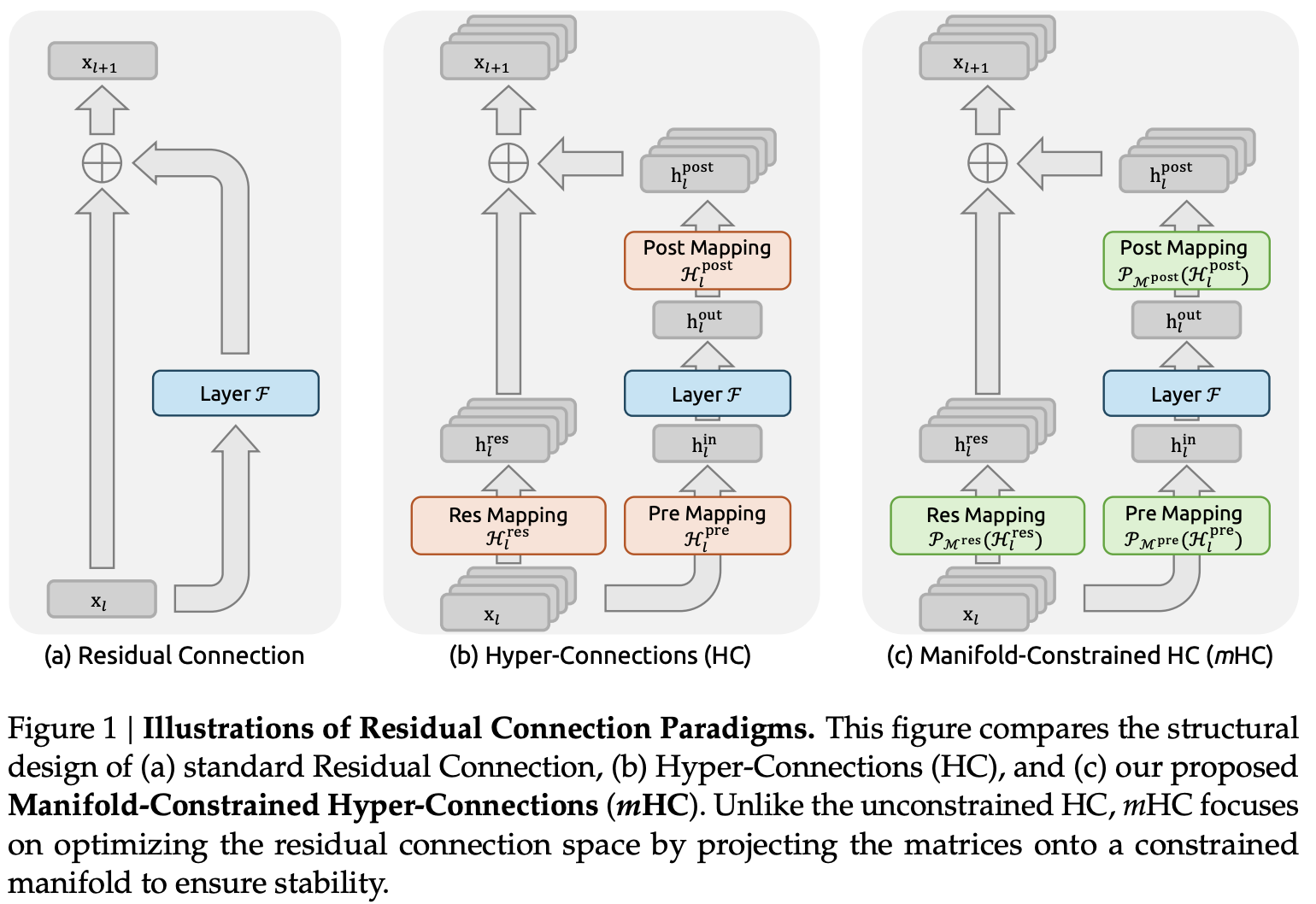
本記事では、このmHCが従来のResidual Connection(残差接続)と何が違うのか、そしてなぜ多様体(Manifold)の概念が次世代LLMにとって重要なのかを、技術的な深掘りを交えて解説する。
背景:高次元空間における「迷子」たち
現代のDeep Learning、特にLLM(Large Language Model)の成功は、残差接続(Residual Connection) に大きく依存している。数式で書けば単純な \(\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l)\) という構造が、勾配消失を防ぎ、超深度のモデル学習を可能にした。
しかし、DeepSeekの研究チームは、この単純な加算が高次元空間におけるデータの「本来の形状」を無視しているという点に着目した。
多様体仮説(Manifold Hypothesis)の再考
「高次元データ(画像や自然言語の埋め込み表現)は、実際には高次元空間内の低次元多様体(Manifold)付近に分布している」という多様体仮説は広く知られている。 従来のResidual Connectionは、ユークリッド空間上での単純なベクトル加算を行う。しかし、データが球面や双曲面のような非ユークリッド的な多様体に乗っている場合、単純な加算 \(\mathbf{x} + \Delta \mathbf{x}\) は、データを多様体から「外へ」押し出してしまうリスクがある。
これが蓄積すると、モデルは本来のデータ構造を見失い、表現力の低下や学習の不安定化(Feature Collapse)を招く。これが、超巨大モデルにおけるスケーリングの壁の一つとなっていた。
mHC:Manifold-Constrained Hyper-Connectionsとは?
mHCの核心は、「層間の信号伝播を、データ多様体の接空間(Tangent Space)または多様体そのものに拘束する」 というアイデアにある。
1. Hyper-Connectionsの定義
通常のSkip Connectionが直前の層(あるいは数層前)からの単純なパスであるのに対し、mHCにおける “Hyper-Connections” は、ネットワークの深さ方向だけでなく、学習された多様体のトポロジーに基づいて動的に決定される接続経路を指す。
数理的には、従来の更新式を以下のように拡張するイメージだ。
\[\mathbf{x}_{l+1} = \Pi_{\mathcal{M}} \left( \mathbf{x}_l + \sum_{k \in \mathcal{N}(l)} \alpha_k \cdot \mathcal{H}_k(\mathbf{x}_k) \right)\]
ここで、\(\Pi_{\mathcal{M}}\) は多様体への射影(Projection)、あるいはリーマン多様体上でのExponential Map (\(\text{Exp}_{\mathbf{x}}\)) に相当する操作である。\(\mathcal{H}\) は通常の重み層ではなく、多様体の曲率(Curvature)を考慮した変換関数として機能する。
2. 幾何学的制約(Manifold Constraint)
論文における最大のブレイクスルーは、この射影 \(\Pi_{\mathcal{M}}\) を計算コストの高い反復法ではなく、学習可能な軽量な制約項として実装した点にある。
具体的には、各層の隠れ状態 \(\mathbf{h}\) に対し、その局所的な固有次元(Intrinsic Dimension)を推定し、次元圧縮と展開を繰り返すAutoencoder的な正則化項を、メインのTransformerブロックと並列に走らせる。これにより、メインストリームの信号が「多様体から逸脱」しようとすると、ペナルティが働き、軌道修正される。
これは、多様体学習(Manifold Learning)の分野で知られる Laplacian Eigenmaps や Diffusion Maps の概念を、静的なデータ解析ではなく、動的なニューラルネットワークのForward Passに組み込んだものと解釈できる。
なぜこれが「Transformerの核心的改良」なのか?
DeepSeekがこのタイミングでmHCを投入した理由は、単なる理論的な美しさだけではない。実用面で極めて大きなメリットがあるからだ。
Feature Collapseの回避と表現力の向上
層が深くなるにつれて、異なるトークンの表現が似通ってしまう「Oversmoothing」問題は、Deep Transformerの宿命であった。mHCは、データを適切な多様体上に留めることで、各トークンの個性を維持したまま、深い抽象化を行うことを可能にする。これにより、特にLong Context(長文脈)における推論能力が劇的に向上する。
学習の安定性と効率化
信号が多様体に沿って流れるということは、最適化の探索空間が制限されることを意味する。無駄な高次元空間(ノイズの海)を探索する必要がなくなるため、収束速度が向上する。DeepSeekのレポートによれば、同等の性能に達するためのTraining Computeを約30%削減できたとされている。
非線形性の獲得
従来のPCA(主成分分析)のような線形な次元削減と異なり、mHCはt-SNEやIsomapのような非線形な構造保存をネットワーク内部で行う。これにより、言語の持つ複雑な意味構造(例:多義語の文脈による使い分けなど)を、より低い次元数で正確に捉えることが可能になる。
実装上の課題と展望
もちろん、mHCには課題もある。最大の懸念は Computational Overhead(計算コストの増大)だ。各ステップで多様体制約を計算することは、単純な行列積に比べて重い処理となる。
しかし、DeepSeekはこの点においても巧妙だ。彼らはmHCを全ての層に適用するのではなく、数層ごとの「チェックポイント」として配置する、あるいは Sparse Hyper-Connections として実装することで、推論速度への影響を最小限に抑えているようだ。これは、彼らが以前DeepSeek-V3で実証した「徹底的なエンジニアリングによる理論の実装」の再来と言える。
まとめ:幾何学的深層学習へのシフト
DeepSeekが提示したmHCは、単なるアーキテクチャの微修正ではない。「ニューラルネットワークを単なる関数近似器として見る」視点から、「データが住まう幾何学的空間の探索機として見る」 視点への転換を促している。
2026年、我々は単にパラメータ数を増やすだけの競争から卒業し、モデルがいかに「賢く」空間を使っているかを議論することになるだろう。mHCはその号砲となる可能性が高い。
参考文献(推測および関連技術)
- DeepSeek AI Team. “DeepSeek-V4 Technical Report: Preliminary findings on mHC.”
- Bronstein, M. M., et al. “Geometric Deep Learning: Grids, Groups, Graphs, Geodesics, and Gauges.” arXiv preprint arXiv:2104.13478 (2021).
- He, K., et al. “Deep Residual Learning for Image Recognition.” CVPR 2016. (Standard ResNet baseline)
- Tenenbaum, J. B., et al. “A Global Geometric Framework for Nonlinear Dimensionality Reduction.” Science 290.5500 (2000). (Isomap / Manifold Learning foundations)